Postulado da multiplicação

É o postulado que determina as regras da multiplicação booleana:

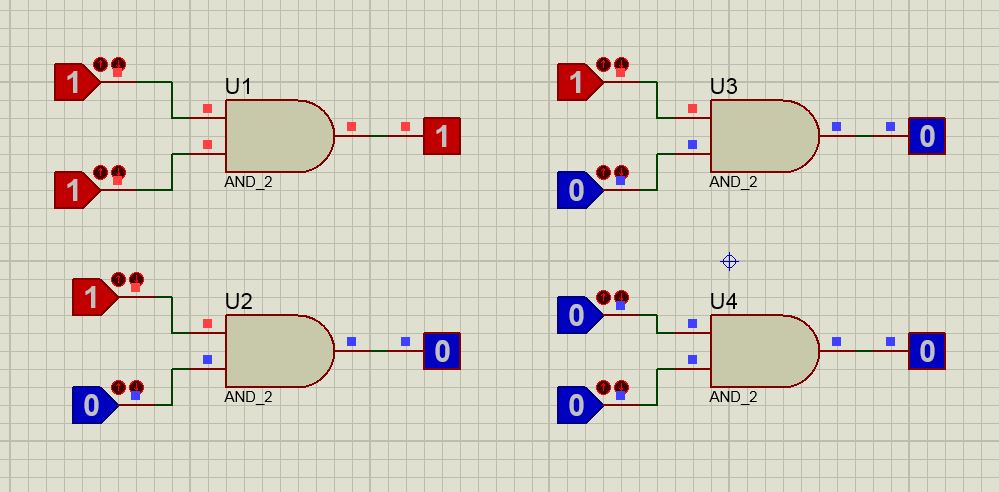
1º) 0 . 0 = 0

2º) 0 . 1 = 0

3º) 1 . 0 = 0

4º) 1 . 1 = 1

Com messe postulado podemos estabelecer as seguintes identidades:

A . 0 = 0  podemos confirmar verificando todas as possibilidades

A = 0         0 . 0 = 0

A = 1         1 . 0 = 0

Notamos que todo número multiplicado por 0 (zero) é 0 (zero).

A . 1 = A  analisando todas as possibilidades:

A = 0          0 . 0 = 0

A = 1          1 . 1 = 1

Notamos que o resultado dessas expressões é sempre igual a A.

A . A = A. Esta identidade, à primeira vista estranha, é verdadeira, como podemos confirmar pela análise de todas as possibilidades:

A = 0          0 . 0 = 0

A = 1          1 . 1 = 1

Notamos que o resultado serão sempre iguais a A.

A . A’ = 0 Vamos analisar todas as possibilidade:

A = 0         0 . 1 = 0

A = 1         1 . 0 = 0

Notamos que para ambos valores possíveis que a variável pode assumir, o resultado da expressão será sempre 0 (zero).

O bloco lógico que executa o postulado da multiplicação é o E (AND).

(Fonte - Livro Sistemas Digitais - Francisco Gabriel Capuano) 

(Fonte - https://www.youtube.com/watch?v=J8nnICpbuPI)